Los elementos de la circunferencia y círculo son la piedra angular dentro de la geometría y las matemáticas en general. Sin embargo, muchas veces se desconoce la diferencia entre una y otra.
¿Qué es un círculo? Un círculo, según la RAE, corresponde al área o superficie plana contenida dentro de una circunferencia.
Esto nos lleva a una segunda interrogante: ¿Qué es una circunferencia? Este elemento corresponde a una figura curva plana y cerrada, cuyos puntos son equidistantes de otro situado en su interior, llamado centro.
La circunferencia se puede representar mediante una ecuación de la forma (x – a)² + (y – b)² = r², donde (a,b) es el centro y r es el radio.
Con estas definiciones claras, las diferencias entre ambas será más sencillo de identificar.
Elementos de la circunferencia y el círculo
Resuelto el enigma sobre la diferencia entre ambas figuras, pasemos a conocer cuáles son sus principales elementos:
1) Centro: es un punto interior equidistante de todos los puntos de la circunferencia. ¿Qué significa equidistante? Que las distancias entre el punto y la figura son iguales.
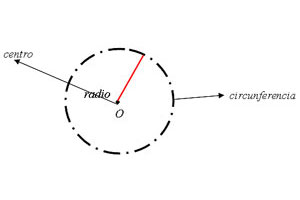
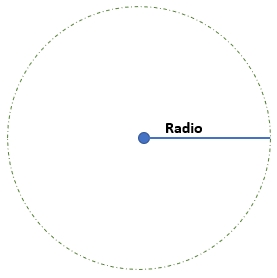
2) Radio: es un segmento que une el centro con un punto de la circunferencia.
¿Cómo se define el radio de una circunferencia?
El radio de una circunferencia es la distancia entre el centro y cualquier punto de la circunferencia. Se representa con la letra r y se puede calcular mediante la fórmula r = d/2, donde d es el diámetro de la circunferencia.
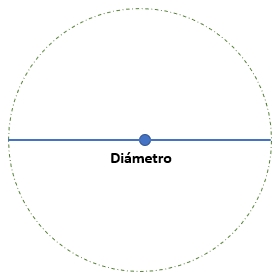
3) Diámetro: es el mayor segmento que une dos puntos de la circunferencia. Corresponde al doble del radio.
¿Cuál es la relación entre el radio y el diámetro de una circunferencia?
El diámetro de una circunferencia es el segmento que une dos puntos de la circunferencia y pasa por el centro. La relación entre el radio y el diámetro es que el diámetro es igual al doble del radio, es decir, d = 2r.
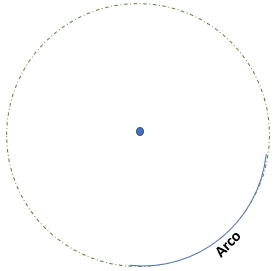
Arco, cuerda, secante y tangente
4) Arco: es un segmento curvilíneo de puntos que pertenecen a la figura circular.
Un arco de una circunferencia es un segmento de la circunferencia que une dos puntos de la misma.
La longitud de un arco se puede calcular mediante la fórmula L = rθ, donde r es el radio de la circunferencia y θ es el ángulo en radianes que abarca el arco.
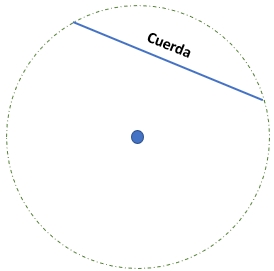
5) Cuerda: es un segmento que une dos puntos dentro de la figura. Las cuerdas con mayor longitud que podemos encontrar son los diámetros.
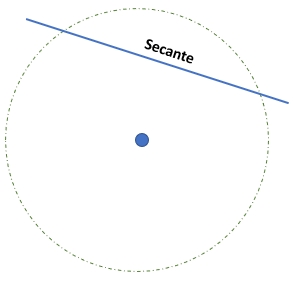
6) Secante: es una recta que corta la circunferencia en dos puntos.
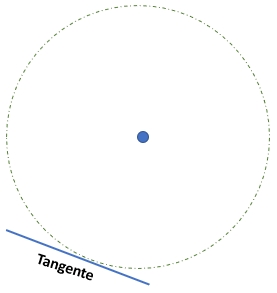
7) Tangente: es una recta que toca esta figura circular en un solo punto. Una tangente es una recta que toca a la circunferencia en un solo punto, llamado punto de tangencia.
Una recta puede ser tangente a una circunferencia en cero, uno o dos puntos.
La posición relativa de una recta y una circunferencia se puede determinar a partir de su número de intersecciones.
Si una recta es tangente a esta figura geométrica, entonces no tiene intersecciones. En cambio si una recta corta a una circunferencia en dos puntos, entonces se dice que es secante.
Si una recta no corta en este elemento circular pero se acerca, entonces se dice que es una recta paralela.
¿Cómo se puede calcular la longitud de una circunferencia?
La longitud de esta figura se puede calcular mediante la fórmula L = 2πr, donde π (pi) es una constante que aproximadamente vale 3,14159.
También se puede calcular utilizando la fórmula L = πd, donde d es el diámetro de la circunferencia.
¿Cuál es la fórmula para calcular el área de un círculo?
El área de un círculo se puede calcular mediante la fórmula A = πr², donde π (pi) es una constante que aproximadamente vale 3,14159 y r es el radio del círculo.







 Sorpresa de Yerbas Buenas
Sorpresa de Yerbas Buenas