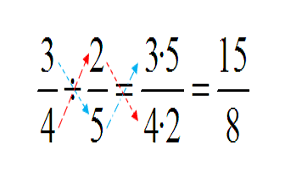Adición
1) Adición de fracciones con igual denominador
Para sumar fracciones cuyo denominador es el mismo, solo debemos sumar los numeradores y conservar el denominador.
Ejemplo:
2) Adición de fracciones con distinto denominador
Para sumar fracciones con distinto denominador, debemos buscar la manera de que ambas fracciones tengan el mismo denominador. Para esto debemos recurrir a la amplificación y simplificación.
Amplificación: consiste en la búsqueda de fracciones equivalentes mediante la multiplicación del numerador y denominador de una fracción por un mismo número.
Busquemos fracciones equivalentes a 
:
Como verás, a través de la amplificación podemos encontrar infinitas fracciones equivalentes a la original.
Simplificación: consiste en la búsqueda de fracciones equivalentes mediante la división exacta del numerador y denominador de una fracción por un mismo número.
Encontremos fracciones equivalentes a 
mediante este método:
La simplificación, nos permite encontrar un menor número de fracciones equivalentes. En nuestro ejemplo solo pudimos encontrar dos.
Ahora que ya sabemos amplificar y simplificar fracciones resolvamos la siguiente adición:
Utilicemos la amplificación para buscar una fracción equivalente a 
con denominador 12:
Cómo es equivalente a 
, podemos sumar entonces:
Utilizando la simplificación: 
(dividimos por 3 el numerador y denominador de la fracción).
Usemos la simplificación para buscar una fracción equivalente a 
con denominador 4. Como podrás darte cuenta no se puede simplificar, es una fracción irreductible, ya que no es posible dividir el numerador y denominador en forma exacta por un mismo número.
Como es equivalente a 
, podemos sumar entonces:
Como verás, a través de la amplificación y simplificación pudimos sumar fracciones con distinto denominador y obtuvimos el mismo resultado.
Una forma fácil de encontrar un denominador común para resolver sumas de fracciones con distinto denominador es la siguiente:
Utilicemos el mismo ejemplo anterior:
Multipliquemos los denominadores de ambas fracciones para obtener un denominador común:
12 x 4 = 48
48 será el denominador común de nuestras nuevas fracciones equivalentes.
Para obtener el numerador de nuestra primera fracción debemos preguntarnos lo siguiente: ¿Por qué número amplificamos el denominador para obtener 48? Es decir, ¿4 multiplicado por qué número nos da 48?
4 multiplicado por 12 es igual 48. Entonces para obtener el numerador de la primera fracción debemos multiplicar 3 por el mismo número, es decir, por 12.
3 x 12 = 36
Ya encontramos la primera fracción equivalente:
Realizamos el mismo procedimiento para encontrar una fracción equivalente a Foto 39 con denominador 48.
12 x 4 = 48 y 4 x 6 = 24, por lo tanto, la segunda fracción con denominador 48:
Ahora podemos sumar:
ahora lo podemos simplificar, con el fin de encontrar una fracción equivalente más pequeña:
Sustracción
1) Sustracción de fracciones con igual denominador
Para restar fracciones cuyo denominador es el mismo, solo debemos restar los numeradores y conservar el denominador.
Ejemplo:
2) Sustracción de fracciones con distinto denominador
Para restar fracciones con distinto denominador, debemos buscar la manera de que ambas fracciones tengan el mismo denominador. Para esto, debemos recurrir a los mismos métodos utilizados en la adición: la amplificación y simplificación de fracciones.
Veamos un ejemplo en el que utilizaremos la amplificación:
Denominador común:
3 x 9 = 27
27 será el denominador común de nuestras nuevas fracciones.
Búsquemos ahora los numeradores:
Numerador minuendo: 3 x ? = 27
? = 9
Ahora multiplicamos 9 por el numerador:
9 x 2 = 18 —-> 18 será el numerador de nuestra primera fracción.
Numerador del sustraendo: 9 x ? = 27
? = 3
Ahora multiplicamos 3 por el numerador:
3 x 3 = 9 —-> 9 será el numerador de nuestra segunda fracción.
A través de la amplificación obtuvimos dos fracciones equivalentes a las originales con denominador común (27):
Ahora que tenemos dos fracciones con el mismo denominador, podemos resolver la sustracción sin problemas, restando los numeradores y manteniendo el denominador:
Simplifiquemos si es posible el resultado de nuestra sustracción:
El resultado en forma simplicada de nuestra sustracción es 
.
